Velocidade significa a qualidade do que é veloz. Designa a rapidez de um movimento ou a celeridade de um processo.
Em Física, velocidade é a relação entre uma determinada distância percorrida e o tempo gasto no percurso. A distância é medida em metros e o tempo em segundo (m/s), no SI (Sistema Internacional de Unidades). A velocidade é uma grandeza vetorial representada por um vetor que possui direção, sentido e módulo.
Em Fotografia, a velocidade do obturador corresponde ao tempo em que permanece aberto o diafragma da câmera expondo o filme (ou sensor) à luz durante a foto. A velocidade controla a quantidade de luz que chega ao sensor alterando o efeito de congelamento (velocidade alta) ou movimento (velocidade baixa) nas fotografias. Quanto mais tempo aberto, mais luz entra e vice-versa.
Velocidade de cruzeiro em um navio ou aeronave significa a velocidade ideal para um determinado percurso, em que se consegue manter a velocidade máxima e constante. Em outros meios de transporte, a velocidade de cruzeiro designa a relação maior eficiência/menor consumo.
A expressão "velocidade de cruzeiro" também é aplicada em outros contextos com o significado de "constante", "sem alteração", "rotineiro" ou "monótono".Na física, velocidade relaciona a variação da posição no espaço em relação ao tempo, ou seja, qual a distância percorrida por um corpo num determinado intervalo temporal. É uma grandeza vetorial, possuindo direção, sentido e módulo, esse último chamado de rapidez e de dimensões [L][T]-1, sendo medida no SI em metros por segundo (m/s ou ms-1). Em geral, os símbolos da velocidade são v ou 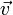 , o primeiro para a velocidade escalar e o segundo para o vetor velocidade. A variação da velocidade em relação ao tempo é a aceleração.
, o primeiro para a velocidade escalar e o segundo para o vetor velocidade. A variação da velocidade em relação ao tempo é a aceleração.
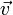 , o primeiro para a velocidade escalar e o segundo para o vetor velocidade. A variação da velocidade em relação ao tempo é a aceleração.
, o primeiro para a velocidade escalar e o segundo para o vetor velocidade. A variação da velocidade em relação ao tempo é a aceleração.Equações de velocidade[editar | editar código-fonte]
Velocidade é um conceito fundamental para a mecânica clássica. Foi a partir desse que os primeiros físicos puderam desenvolver o estudo do movimento dos corpos, tornando-se capazes de descrever trajetórias através de funções matemáticas. Isaac Newton, pai da mecânica clássica, desenvolveu o cálculo diferencial a partir desse estudo. Há dois tipos de movimentos considerados mais simples: o movimento retilíneo uniforme(MRU) e o movimento retílineo uniformemente variado(MRUV), que são representados por equações lineares e quadrádicas respectivamente. Para outros tipos de movimento mais complexos utiliza-se a derivada.
Movimento retilíneo uniforme[editar | editar código-fonte]
É o movimento descrito por objetos com velocidade constante em uma trajetória retilínea (em linha reta), para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula. Dado um deslocamento 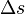 , em um intervalo de tempo
, em um intervalo de tempo  A velocidade escalar
A velocidade escalar  é dada por:
é dada por:
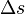 , em um intervalo de tempo
, em um intervalo de tempo  A velocidade escalar
A velocidade escalar  é dada por:
é dada por: .
.
Somente no MRU a velocidade de um corpo a qualquer instante é igual à sua velocidade média, sabendo-se a posição e velocidade da partícula em um determinado instante permite determinar a localização da partícula em qualquer outro instante.1
A equação do espaço  em função do tempo
em função do tempo 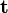 , a partir de um ponto
, a partir de um ponto  é:
é:
 em função do tempo
em função do tempo 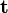 , a partir de um ponto
, a partir de um ponto  é:
é:
O gráfico sxt desse movimento é uma linha reta2 cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo 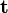 é o valor da velocidade.
é o valor da velocidade.
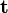 é o valor da velocidade.
é o valor da velocidade.Movimento retilíneo uniformemente variado[editar | editar código-fonte]
É o movimento de objetos que variam sua velocidade de forma constante, ou seja, possuem aceleração constante.
No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.
E a equação do espaço é a seguinte:
O gráfico sxt desse movimento é uma parábola.
Veja mais em movimento retilíneo.
Derivada[editar | editar código-fonte]
Os dois movimentos acima só ocorrem em condições muito específicas. Para estudar os movimentos dos corpos como ocorrem na natureza, Isaac Newton desenvolveu a derivada. Para calcular a velocidade instantânea de um corpo em certo instante é necessário usar limite, medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.
Da definição de derivada:
Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico sxt, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea.
A aceleração é a derivada da velocidade com relação ao tempo:3
Unidades de velocidade[editar | editar código-fonte]
Sistema Internacional de Unidades (SI)[editar | editar código-fonte]
- Metro por segundo (m/s): unidade de velocidade do SI (1 m/s = 3,6 km/h).
Sistema CGS de unidades[editar | editar código-fonte]
- Centímetro por segundo (cm/s)
Sistema imperial de medidas[editar | editar código-fonte]
- Pé por segundo (ft/s)
- Milha por hora (mph)
- Milha por segundo (mps)
[editar | editar código-fonte]
- O nó é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma milha náutica por hora.
Aeronáutica[editar | editar código-fonte]
- O Número de Mach (M ou Ma) é uma medida de velocidade relativa que se define como o quociente entre a velocidade dum objeto e a velocidade do som no meio em que se move dito objeto. É um número adimensional tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h).
Unidades naturais[editar | editar código-fonte]
- Velocidade da luz no vácuo = 299 792 458 m/s (convencionalmente 300 000 km/s). É a maior velocidade que se pode atingir no Universo segundo a Teoria Restrita da Relatividade de Einstein.
Outras unidades[editar | editar código-fonte]
- Quilômetro por hora (km/h)
- Quilômetro por segundo (km/s)
Referências
- ↑ LOPES, Helio; MALTA, Iaci; PESCO, Sinésio. Cálculo a uma variável - vol. II: Derivada e integral. [S.l.]: Edições Loyola, 2002. ISBN 9788515024452
- ↑ PARETO, Luis. Mecânica e Cálculo de Estruturas. [S.l.]: Hemus. ISBN 9788528905007
- ↑ Neto, João Barcelos. Mecânica Newtoniana, Lgrangiana e Hamiltoniana. [S.l.]: Editora Livraria da Fisica, 2004. ISBN 9788588325265









Nenhum comentário:
Postar um comentário