FUNÇAO CONTINUA

Em matemática, uma função é contínua quando, intuitivamente, as pequenas variações nos objectos correspondem a pequenas variações nas imagens. Nos pontos onde a função não é contínua, diz-se que a função é descontínua, ou que se trata de um ponto de descontinuidade.

Índice

  [esconder] 

• 1Definições de continuidade
  • 1.1Em espaço topológico
    • 1.1.1Exemplos
  • 1.2Em espaço métrico
    • 1.2.1Exemplo
  • 1.3Equivalência das definições
  • 1.4Em termos de limites
• 2Função sequencialmente contínua
• 3Propriedades
• 4Referências

Definições de continuidade[editar | editar código-fonte]

Em espaço topológico[editar | editar código-fonte]

Diz-se que uma função ${\displaystyle f:X\rightarrow Y}$ entre espaços topológicos é contínua se a imagem recíproca de qualquer aberto de ${\displaystyle Y}$ é um aberto de ${\displaystyle X.}$

Exemplos[editar | editar código-fonte]

Esta função é descontínua nos inteiros.

Estes exemplos usam propriedades da imagem recíproca, ou seja, dada uma função ${\displaystyle f:X\rightarrow Y}$ e um conjunto ${\displaystyle A\subset Y,}$ o conjunto ${\displaystyle f^{-1}(A)=\{x\in X|f(x)\in A\}.}$

• Seja ${\displaystyle X}$ um conjunto com a topologia discreta ${\displaystyle \tau _{X}=P(X),}$ ${\displaystyle Y}$ com qualquer topologia, então qualquer função ${\displaystyle f:X\rightarrow Y}$ é contínua.

Basta ver que, ${\displaystyle \forall A\in Y}$ aberto temos que, ${\displaystyle f^{-1}(A)\in P(X),}$ e portanto é aberto, o que mostra que ${\displaystyle f}$ é uma função contínua.

• Seja ${\displaystyle Y}$ um conjunto com a topologia grosseira ${\displaystyle \tau _{Y}=\{\varnothing ,Y\},}$ ${\displaystyle X}$ com qualquer topologia, então qualquer função ${\displaystyle f:X\rightarrow Y}$ é contínua.

De fato, pois, como os dois únicos abertos de ${\displaystyle \tau _{Y}}$ são ${\displaystyle \varnothing }$ e ${\displaystyle Y,}$ basta verificar se suas imagens inversas são abertos. Mas ${\displaystyle f^{-1}(\varnothing )=\varnothing }$ e ${\displaystyle f^{-1}(Y)=X,}$ e, por definição, ${\displaystyle \varnothing }$ e ${\displaystyle X}$ são abertos em qualquer topologia em ${\displaystyle X.}$

• Sejam ${\displaystyle f:X\rightarrow Y}$ e ${\displaystyle g:Y\rightarrow Z}$ funções contínuas. Então ${\displaystyle g\circ f:X\rightarrow Z}$ também é uma função contínua.

Fato pois: qualquer que seja ${\displaystyle A\subset Z}$ aberto, pela continuidade de ${\displaystyle g,}$ temos que ${\displaystyle g^{-1}(A)}$ é um aberto em ${\displaystyle Y.}$ Portanto, pela continuidade de ${\displaystyle f,}$ ${\displaystyle f^{-1}(g^{-1}(A))}$ é um aberto em ${\displaystyle X.}$ Mas ${\displaystyle f^{-1}(g^{-1}(A))=(g\circ f)^{-1}(A),}$ o que prova a continuidade de ${\displaystyle g\circ f.}$

Em espaço métrico[editar | editar código-fonte]

Diz-se que uma função ${\displaystyle f}$ é contínua no ponto ${\displaystyle x=a}$ se ${\displaystyle a}$ é um ponto isolado do domínio ou, caso seja ponto de acumulação de ${\displaystyle X,}$ se existir o limite de ${\displaystyle f(x)}$ com ${\displaystyle x}$ tendendo a ${\displaystyle a}$ e esse limite for igual a ${\displaystyle f(a).}$

OBS.: Não faz sentido calcular limites em pontos que não são de acumulação. Caso insistíssemos teríamos que qualquer valor seria limite de ${\displaystyle f(x)}$ com ${\displaystyle x}$ tendendo a ${\displaystyle a}$

Em análise real, essa definição é escrita na forma tradicional Epsilon-Delta, ou seja, diz-se que uma função ${\displaystyle f}$ é contínua num ponto ${\displaystyle a}$ do seu domínio se, dado ${\displaystyle \epsilon >0,\exists \delta >0}$ tal que ${\displaystyle \forall x\in X,a-\delta <x<a+\delta }$ então ${\displaystyle f(a)-\epsilon <f(x)<f(a)+\epsilon .}$

Esta definição, com uma pequena adaptação, pode ser usada para uma função de um espaço métrico ${\displaystyle E}$ em outro espaço métrico ${\displaystyle F:}$ a função ${\displaystyle f}$ é contínua em ${\displaystyle a\in E}$ quando dado ${\displaystyle \epsilon >0,\exists \delta >0}$ tal que ${\displaystyle \forall x\in E,d_{E}(x,a)<\delta \rightarrow d_{F}(f(x),f(a))<\epsilon .}$

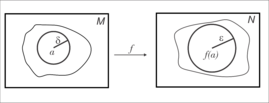
Em termos de bolas, dados dois espaços métricos ${\displaystyle M,N}$ dizemos que a aplicação ${\displaystyle f:M\longrightarrow N}$ é contínua em ${\displaystyle a\in M}$ se, dada uma bola aberta ${\displaystyle B'=B(f(a),\epsilon )}$ de centro ${\displaystyle f(a)}$ e raio ${\displaystyle \epsilon }$ pode-se encontrar uma bola ${\displaystyle B=B(a,\delta ),}$ de centro ${\displaystyle a}$ e raio ${\displaystyle \delta }$ tal que ${\displaystyle f(B)\subset B'.}$ ^[1]

Diz-se que f é contínua em seu domínio, ou simplesmente contínua, se ela for contínua em todos os pontos desse domínio.

Exemplo[editar | editar código-fonte]

• Seja ${\displaystyle f:X\longrightarrow Y,}$ ${\displaystyle X}$ e ${\displaystyle Y}$ espaços métricos não vazios. Se ${\displaystyle \forall x,y\in X}$ tivermos que ${\displaystyle d(f(x),f(y))\leq c\cdot d(x,y),}$ então a aplicação ${\displaystyle f}$ é contínua e a constante ${\displaystyle c}$ é chamada de constante de Lipschitz. Na reta Real toda aplicação Lipschitiziana é uniformemente contínua.

Equivalência das definições[editar | editar código-fonte]

Se ${\displaystyle E}$ e ${\displaystyle F}$ são espaços métricos, e ${\displaystyle \tau _{E}{\mbox{ e }}\tau _{F}}$ as topologias geradas pelas métricas em ${\displaystyle E}$ e ${\displaystyle F,}$ então uma função ${\displaystyle f:E\rightarrow F}$ é contínua pela definição topológica se, e somente se, ela é contínua pela definição métrica.

Em termos de limites[editar | editar código-fonte]

Uma função ${\displaystyle f(x)}$ é dita ser contínua em um ponto ${\displaystyle a}$ de seu domínio se:

$${\displaystyle \lim _{x\to a}f(x)=f(a)}$$

Observa-se que esta definição exige que o limite à esquerda exista assim como o limite da direita e que a função esteja definida no ponto com o mesmo valor de limite para o ponto.

Função sequencialmente contínua[editar | editar código-fonte]

Uma função ${\displaystyle f:E\rightarrow F,}$ em que ${\displaystyle E}$ e ${\displaystyle F}$ são espaços topológicos, é sequencialmente contínua em um ponto ${\displaystyle a\in E}$ quanto ela comuta com o limite de sequências, ou seja, quando para toda sequência ${\displaystyle x_{i}\in E}$ cujo limite (em ${\displaystyle E}$) seja ${\displaystyle a,}$ temos que o limite (em ${\displaystyle F}$) de ${\displaystyle f(x_{i})}$ é ${\displaystyle f(a).}$ Uma forma elegante de escrever isso é ${\displaystyle \lim _{i\rightarrow \infty }f(x_{i})=f(\lim _{i\rightarrow \infty }x_{i}).}$

Propriedades[editar | editar código-fonte]

• Função Composta: Se ${\displaystyle f:E\to F}$ e ${\displaystyle g:F\to G}$ são funções contínuas, então é imediato (pela definição topológica) que a função composta ${\displaystyle g\circ f:E\to G}$ é contínua.
• Se ${\displaystyle f:X\rightarrow Y}$ é uma bijeção contínua de um espaço topológico compacto ${\displaystyle X}$ em um espaço topológico de Hausdorff ${\displaystyle Y,}$ então ${\displaystyle f}$ é um homeomorfismo.
• O conjunto dos zeros de uma aplicação contínua entre um espaço topológico ${\displaystyle X}$ e a reta real ${\displaystyle \mathbb {R} ,}$ com a topologia usual, é um conjunto fechado. Em particular, o conjunto das matrizes singulares é fechado em ${\displaystyle \mathbb {R} ^{n\times n},}$ pois o determinante define uma aplicação contínua nesse espaço.
• Sejam ${\displaystyle X}$ e ${\displaystyle Y}$ dois espaços topológicos, ${\displaystyle U\subset X}$ e ${\displaystyle f:X\rightarrow Y}$ uma aplicação contínua. Então ${\displaystyle f}$ restrita a ${\displaystyle U}$ ainda é uma aplicação contínua.

[Esconder] v • e Tópicos sobre análise
Cálculo: Integração Diferenciação Equações diferenciais (ordinária - parcial) Teorema fundamental do cálculo Cálculo de variações Cálculo vetorial Cálculo tensorial Tábua de integrais Tabela de derivadas
Análise real Análise complexa Análise funcional Análise de Fourier Análise harmônica Teoria da medida Teoria de representação Funções Função contínua Funções especiais Limite Séries Infinito

Referências[editar | editar código-fonte]

• Munkres, J. (1966). Elementary Differential Topology, edição revisada. Annals of Mathematics Studies 54. Princeton University Press. ISBN 0-691-09093-9
• Lima, Elon Lages (2013). Análise Real - Funções de uma variável. Coleção Matemática Universitária. 1 12ª ed. IMPA. 198 páginas. ISBN 978-85-244-0048-3

1. Ir para cima↑ LAGES, Elon (1977). Espaços métricos. Rio de Janeiro: IMPA. 32 páginas

•  Portal da matemática

Categorias: 

• Análise matemática
• Topologia
• Cálculo