segunda-feira, 12 de outubro de 2015

RESONANCIA

Em física, ressonância é a tendência de um sistema a oscilar em máxima amplitude em certas frequências conhecidas como frequências ressonantes ou frequências naturais do sistema. Nessas frequências, até mesmo forças periódicas pequenas podem produzir vibrações de grande amplitude, pois o sistema armazena energia vibracional.
Um oscilador harmônico simples possui uma frequência angular natural relacionada com as características do sistema em questão. Quando o oscilador harmônico simples está sujeito a uma força externa periódica e contínua, o denominamos de oscilador forçado. Dependendo da frequência dessa força, pode ocorrer efeito ressonante.
Interpretaremos em um primeiro momento a ressonância de maneira idealizada, ou seja, não levaremos em conta as perdas de energia ocasionadas por atrito, por exemplo. Então, de maneira simplificada, a ressonância ocorre em um sistema quando o mesmo está sujeito a uma força externa contínua e periódica cuja periodicidade está diretamente relacionada com a frequência natural do sistema. Nesse caso, o sistema produzirá grandes amplitudes.
Contudo, a realidade não é tão simples, existem algumas perdas de energia de período a período, a qual denominamos de amortecimento. Quando o amortecimento é pequeno, a frequência de ressonância do sistema é aproximadamente igual à frequência natural do sistema.
Os sistemas possuem múltiplas e distintas frequências de ressonância e esse fenômeno ocorre com todos os tipos de vibrações ou ondas; mecânicas (acústicas), eletromagnéticas, e funções de onda quântica. Sistemas ressonantes podem ser usados para gerar vibrações de uma frequência específica, ou para obter frequências específicas de uma vibração complexa contendo muitas frequências.
A ressonância foi descoberta por Galileu Galilei quando começou suas pesquisas com pêndulos e cordas musicais no começo de 1602. Outros acreditam que Pitágoras foi o pioneiro no assunto muito antes durante sua vida entre 570 - 495 anos a.C. especialmente na investigação sobre teorias musicais.

Exemplos[editar | editar código-fonte]

  • Ressonância mecânica
  • Ressonância elétrica
  • Ressonância óptica
  • Ressonância orbital em astronomia.
  • Ressonância Molecular

Oscilações forçadas[editar | editar código-fonte]

Com o intuito de apresentar uma base introdutória clara sobre ressonância, e para fins práticos, falaremos sobre ressonância no que concerne a perspectiva de osciladores harmônicos forçados. A ressonância elétrica possui a mesma equação que a ressonância em um sistema massa-mola, porém, com outras variáveis. Esse exemplo ilustra o fato de que a equação de ressonância é a mesma tanto para o caso elétrico, para o caso mecânico, quanto para os demais casos, a não ser pelas respectivas variáveis.[1]

Descrição teórica da ressonância em oscilações forçadas[editar | editar código-fonte]

A criança no balanço constitui um caso de oscilação livre se ela não receber nenhum tipo de empurrão, caso contrário, constituiria um caso de oscilação forçada
Uma criança que se diverte em um balanço sem que ninguém a empurre constitui um exemplo de oscilação livre. Contudo, se a esse movimento for acrescentado uma força externa periódica, dizemos que a criança estará executando uma oscilação forçada, e dependendo da frequência da força a amplitude do movimento pode aumentar ou diminuir. Como veremos a seguir, a amplitude aumentará quando a frequência da força externa é a mesma da frequência natural do sistema. É o caso que aplicamos uma força externa periódica - empurramos a criança toda vez que o balanço se encontrar no máximo de altura (máxima energia potencial - com a mesma frequência do movimento livre.[2]
A amplitude do oscilador forçado varia quando a frequência angular da força externa varia. Percebemos que a amplitude é máxima quando a razão entre a frequência angular natural do sistema e a frequência angular da força externa é um.
A um sistema que executa oscilações forçadas podemos associar duas frequências angulares (as relações matemáticas entre os termos físicos estão explicitados abaixo): uma delas está de acordo com a frequência angular das oscilações livres do sistema, ou seja, é a frequência natural do sistema adquirido a partir de uma perturbação curta; e a outra está associada com a frequência angular da força externa (contínua e periódica) que produz a oscilação forçada.[2] Note que em um momento falamos sobre frequência angular natural e em outro apenas sobre frequência natural. Isso se deve pelo fato de que as duas grandezas estão relacionadas por uma constante {2\pi}, descritas a seguir:
f_0 = \frac{\omega_0}{2\pi}
A amplitude do sistema de oscilação forçada ideal é máxima quando a frequência angular da força externa é igual à frequência angular natural do sistema. Essa situação caracteriza um caso de ressonância, na qual o sistema passa a oscilar com um amplitude crescente. Na verdade, como veremos na interpretação matemática, essa amplitude seria infinita. O sistema não atinge essa amplitude devido a alguns outros termos de atrito e resistência do material que não foram considerados.[1]
Ressonância em ondas estacionárias
Para um sistema que sofre oscilação forçada com amortecimento (caso real), percebemos que o menor amortecimento está associado a um pico de ressonância mais alto. Esse caso está ilustrado no gráfico ao lado.
Apesar de termos usado o exemplo particular da criança no balanço como interpretação simplificada da ressonância, podemos generalizar as implicações para outros diversos casos em muitos campos diferentes, e também perceberíamos que as equações seriam as mesmas. Existem muitas situações na natureza na qual algo está oscilando e na qual o fenômeno de ressonância ocorre.[1] Todas as estruturas mecânicas possuem uma ou mais frequências naturais de vibração. Se a estrutura é submetida a forças periódicas de mesma frequência ou próxima a frequência natural pode ocorrer o efeito de ressonância, de forma mais brusca ou não dependendo do amortecimento do sistema, e isso pode causar a ruptura da estrutura.[2] Para efeitos de interpretação, a força externa poderia ser a força causada por um terremoto, nesse caso.

Descrição matemática da ressonância em oscilações forçadas[editar | editar código-fonte]

Requisitos[editar | editar código-fonte]

F = ma = m \frac{\mathrm{d}^2x}{\mathrm{d}t^2}
F = -k x \,
  • A frequência das oscilações será dada pela seguinte relação:
\displaystyle f = \frac {\omega_0} {2 \pi} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}
  • Identidades:
{\omega_0} : frequência natural do sistema em questão; {\omega} : frequência da força externa;
  • Se definirmos {\omega_0}^2 = k/m, então a a equação do oscilador harmônico simples poderá ser escrita do seguinte modo:
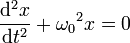
\frac{\mathrm{d}^2x}{\mathrm{d}t^2} + {\omega_0}^2 x = 0
  • Solução homogênea da equação do oscilador harmônico simples:
x(t) = C_1 \sin{\omega_0 t} + C_2 \cos{\omega_0 t} \,

Descrição matemática[editar | editar código-fonte]

A seguir discutiremos o oscilador harmônico forçado. A equação então é a seguinte:
m \frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -k x + F_e
Sabemos que a solução da parte homogênea dessa equação diferencial, ou seja, a solução (usando \scriptstyle {\omega_0}^2 = k/m) de:
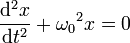
\frac{\mathrm{d}^2x}{\mathrm{d}t^2} + {\omega_0}^2 x = 0
é:
x_H(t) = C_1 \sin{\omega_0 t} + C_2 \cos{\omega_0 t} \,
Precisamos descobrir qual é a solução particular referente a força externa \scriptstyle F_e(t).
A força externa pode ter diversos tipos de dependências funcionais com diferentes frequências. Tentaremos resolver a equação com uma força especial, uma força oscilante:
F_e(t) = F_0 \cos{\omega t} \,
Note que \scriptstyle {\omega} não é necessariamente o mesmo que \scriptstyle {\omega_0}. Temos \scriptstyle {\omega} sob o nosso controle; Então devemos resolver tal equação. Com conhecimento prévio de equações diferenciais percebemos que uma solução particular é do tipo:
x_P(t) = C_3 \cos{\omega t} \,  , onde a constante é para ser determinada.
Então jogamos essa solução \scriptstyle x_P(t) na equação do oscilador harmônico forçado com \scriptstyle F_e(t) explicito. Colocamos também \scriptstyle {\omega_0}^2m = k e encontraremos:
-m {\omega}^2 C_3 \cos{\omega t} \, = -m {\omega_0}^2 C_3 \cos{\omega t} \, + F_0 \cos{\omega t} \,
Como o cosseno aparece em todos os lugares, podemos dividir a equação toda por ele e mostrar que a solução especial \scriptstyle x_P(t) = C_3 \cos{\omega t} \,  é, de fato, uma solução, se escolhermos o \scriptstyle C_3 corretamente. A resposta é que \scriptstyle C_3 deve ser
Ressonância
C_3=F_0/m({\omega_0}^2-{\omega}^2)
Então a solução particular é:
x_P(t)=F_0\cos({\omega t}) \,/m({\omega_0}^2-{\omega}^2)
De fato, a solução geral do oscilador harmônico forçado será a soma da solução particular com a solução da equação homogênea:
x_G(t) = C_1 \sin{\omega_0 t} + C_2 \cos{\omega_0 t} \, + F_0\cos({\omega t}) \,/m({\omega_0}^2-{\omega}^2)
Notemos, então, que quando a frequência angular da força externa se aproxima do valor da frequência angular natural do sistema sob oscilação livre, teremos um fator periódico com uma amplitude que tende ao infinito. Sabemos que não existe nenhum sistema que chegaria a esse ponto, pois além dele se partir antes, existem outros termos de atrito e outras forças que não consideramos por fins práticos mas que acontecem no tempo real. [1] Ao somarmos a solução particular com a solução do caso homogêneo, percebemos que existe a concordância com o Princípio da Superposição das Ondas. Podemos interpretar essa situação, em que o sistema não pode atingir uma amplitude infinita, pela perspectiva do Princípio da Superposição das Ondas: só pode existir a sobreposição de ondas até o momento que o sistema em questão permitir, ou seja, o quanto a estrutura do material suporta, por exemplo.[2] De fato estamos interessados no resultado qualitativo de tal equação. Chegamos num resultado que está de acordo com a explicação teórica acima e que configura o efeito de ressonância.
Descrição matemática 2[editar | editar código-fonte]
Podemos, também, interpretar o caso de ressonância a partir de uma força externa periódica que já tenha a mesma frequência angular natural do sistema[3] , o que é diferente do primeiro caso, no qual consideramos que a força externa não possuía a mesma frequência angular natural do sistema, mas que a fazíamos assumir o valor ao analisarmos a solução geral. Então, a partir dessa perspectiva, podemos considerar a força externa como:
F_e(t) = F_0 \cos{\omega_0 t} \,
Assim, percebemos que existe uma similaridade dessa solução, com a solução que já conhecemos da parte homogênea que é:
x_H(t) = C_1 \sin{\omega_0 t} + C_2 \cos{\omega_0 t} \,
Com o conhecimento de equações diferenciais é fácil perceber que a solução particular referente a força externa precisa ser da seguinte forma para produzirmos soluções linearmente independentes:
\scriptstyle x_P(t) = C_3t \cos{\omega_0 t} \,  , onde a constante é para ser determinada. Substituindo a equação da solução particular na equação do sistema, encontramos a seguinte constante referente a força externa:
C_3=F_0t/2m{\omega_0}
Então, a solução geral é da forma[3] :
x_H(t) = C_1 \sin{\omega_0 t} + C_2 \cos{\omega_0 t} \, + F_0t\sin({\omega_0 t} \,)/2m{\omega_0}
E, novamente, percebemos que a força externa passa a governar o sistema se se considerar tempos sucessivos, na qual a amplitude do termo periódico na solução geral, referente a força externa, só tende a aumentar com o decorrer do tempo. Chegamos, mais uma vez, num resultado que está de acordo com a explicação teórica acima e que configura o efeito de ressonância.

Ver também[editar | editar código-fonte]

Referências

  1. ↑ Ir para:a b c d Feynman, Leighton & Sands. Lições de Física: Volume 1, 2ª Edição. Editora: bookman
  2. ↑ Ir para:a b c d Halliday & Resnick. Fundamentos de Física: Gravitação, Ondas e Termodinâmica, 8ª Edição. Editora: LTC
  3. ↑ Ir para:a b Boyce & DiPrima. Equações Diferenciais Elementares. 8ª Edição. Editora LTC.Antes de falarmos sobre ressonância, existem algumas coisas que precisamos entender. Uma delas é a frequência, que é uma grandeza física associada a movimentos de característica ondulatória que indica o numero de execuções (ciclos ou oscilações) por unidade de tempo. O tempo necessário para executar uma oscilação é o período f = 1/T.
    Existe ainda a frequência natural, que será um termo muito usado para nós entendermos o que acontece quando falamos em ressonância.
    Quando alguém deixa uma chave inglesa cair no chão, nós provavelmente não confundiremos o som emitido com o de um taco de beisebol ao bater no chão. Isso é porque os dois objetos vibram de maneira diferente quando colidem. Qualquer objeto formado por um material elástico, quando perturbado, vibrará com seu próprio conjunto de frequências particulares, que juntas formam seu som próprio. Essa é então a frequência natural de um objeto, a qual depende de um conjunto de fatores tais como a elasticidade e a forma do objeto.
    Agora sim, vamos falar de Ressonância!
    Quando a frequência da vibração forçada de um objeto se iguala à frequência natural dele, ocorre um drástico aumento da amplitude. Esse fenômeno é denominado Ressonância. Literalmente Ressonância significa “ressoar” ou “soar novamente”. Uma massa de modelar não ressoa por não ser elástica, e um lenço que deixamos cair é flácido demais. Para alguma coisa ressoar, é necessário uma força que a traga de volta a sua posição original e bastante energia para mantê-la vibrando.
    Uma experiência comum que ilustra a Ressonância pode ser realizada com o balanço de uma criança. Quando fazemos esse brinquedo oscilar, o fazemos num ritmo igual a sua frequência natural. Mesmo pequenos empurrões dados, se dados em ritmo com a frequência natural do balanço, produzirão grandes amplitudes.
    A ressonância não se restringe ao movimento ondulatório. Ela ocorre sempre que impulsos sucessivos são aplicados sobre um objeto vibrante, em ritmo com sua frequência natural. Em 1831, tropas de cavalaria marchando ao longo de uma ponte para pedestres próxima a Manchester, Inglaterra, inadvertidamente causaram o colapso da ponte quando o ritmo da marcha se igualou à frequência natural da estrutura. Desde então, tornou-se costume ordenar às tropas que ‘percam o passo’ ao atravessar pontes.
    Os efeitos da ressonância estão ao nosso redor. A ressonância está por trás não apenas dos sons musicais, mas da cor das folhas durante o outono, da altura das marés oceânicas, do funcionamento dos lasers e de uma vasta variedade de fenômenos.
    O ‘som das ondas do mar’ que você ouve quando encosta seu ouvido em uma concha é produzido por ressonância. O ruído do som do ar ao lado de fora da concha é uma mistura de ondas sonoras com quase todas as frequências audíveis, forçando a oscilação do interior da concha. A concha funciona como um órgão, contendo um conjunto de frequências naturais, portanto o ar no interior da concha oscila com mais intensidade nessas frequências, produzindo o som que você ouve.
    Temos ainda, o exemplo que foi citado na nossa seção de curiosidades, quando uma cantora quebra uma taça ao emitir som. Uma taça de cristal de boa qualidade possui frequências naturais que você pode ouvir dando umas batidas na taça. Quando a cantora emite uma nota em volume muito alto, numa frequência exatamente igual a uma das frequências da taça, as oscilações que ocorrem podem se superpor, dando origem a uma oscilação com amplitude muito elevada, que fará a taça vibrar e se quebrar.Qual seria a melhor maneira de visualizar o interior do corpo humano? Abri-lo, não é verdade? Mas isso não é mais necessário. Conectado a um computador, o aparelho de ressonância magnética fornece “fotografias” tão nítidas do interior do corpo que permitem ao médico ter uma excelente visão dele. Ainda mais: pode virtualmente fatiá-lo e fornecer “fotografias” de cada uma dessas fatias. Assim, a ressonância magnética tornou-se o mais moderno e o mais perfeito exame de diagnóstico por imagem, fornecendo imagens em alta definição dos órgãos internos do corpo através da utilização de um campo magnético. Ela consegue detectar anomalias que os exames anteriores não conseguiam, além de fornecer imagens mais detalhadas que as que se consegue com outros métodos de exame. O aparelho em que o exame é feito consta de um tubo circundado por um grande imã, no interior do qual é produzido um potente campo magnético.
    Como realizar o exame de ressonância magnética?
    Geralmente o exame não exige nenhum preparo prévio (às vezes, de acordo com o exame a ser realizado, pode ser solicitado um jejum de 4 a 6 horas) e tão logo terminado o procedimento, o paciente pode retomar suas atividades normais. Não é necessário interromper qualquer medicação que o paciente esteja tomando.
    A pessoa que passa pelo exame de ressonância magnética deita-se numa maca e é orientada a ficar imóvel, enquanto, por deslizamento, é introduzida dentro de um tubo constituinte do aparelho. Como os movimentos impossibilitam a captação de imagens precisas, as crianças e os pacientes que não consigam se controlar necessitam ser sedados antes do exame.
    O exame pode durar de 15 minutos até mais de uma hora, dependendo do objetivo. A ressonância magnéticanão utiliza radiação, porém uma vez que o aparelho gera um potente campo magnético (10.000 vezes maior que o campo magnético da terra), é preciso tomar certos cuidados durante o exame e mesmo fora dele. Pequenos objetos metálicos podem se transformar em projéteis ao serem atraídos pelo campo magnético da ressonância. Mesmo objetos grandes e pesados, como estantes e bancos presentes na sala, podem ser atraídos. O fato de ser submetido a esse campo magnético não acarreta nenhum dano biológico ao ser humano, mas o técnico ou o médico que realiza a ressonância magnética deve dar aos pacientes instruções detalhadas, entre as quais:
    • O paciente deve ir ao banheiro antes do exame para que não experimente nenhuma urgência durante o mesmo, que pode durar um período longo.
    • O paciente não deve se mexer durante todo o exame, mas pode se comunicar com o médico para pedir ou receber instruções ou relatar o que estiver sentindo.
    • A ressonância é um procedimento ruidoso. O paciente deve usar um protetor ou fone de ouvidos, geralmente oferecido pela instituição que faz o exame.
    • Alguns pacientes com perfil fóbico podem se sentir incomodados no interior do tubo de ressonância magnética ou mesmo se recusarem a entrar nele. Em casos mais intensos, ele pode optar por um aparelho aberto ou ser submetido a uma sedação rápida, embora isso signifique introduzir uma complicação a mais numa técnica relativamente inócua.
    • A roupa usada no exame não pode conter metais (como botões e fivelas).
    • Alfinetes, grampos de cabelo e zíper de metal podem distorcer as imagens da ressonância magnética e também devem ser retirados.
    • Aparelhos e objetos como cartões de crédito, relógios, óculos, aparelhos de surdez, celulares, próteses ortodônticas móveis e piercings devem ser retirados, mas aparelhos ortodônticos fixos não representam riscos para o paciente, embora possam prejudicar a qualidade das imagens.
    • Antes do exame devem ser informados ao médico, para que ele decida sobre a possibilidade ou não do exame, o uso de clipes de aneurismas cerebrais, marca-passos cardíacos, prótese coclear, fragmentos de metal no corpo, implantes oculares etc.
    • Outros dispositivos, como DIU, clipes de cirurgias da vesícula, válvulas cerebrais, implantes ortopédicos e stents vasculares implantados há mais de seis semanas podem ser admitidos sem problemas.
    • Por medida de segurança, mulheres grávidas só devem se submeter ao exame depois da 12ª semana degravidez. Não são conhecidos malefícios para a mãe ou para o feto mesmo nas ressonâncias realizadas antes desse período.
    • O limite de peso para o exame é de 160 quilos.
    • Em alguns exames vasculares é necessária a aplicação de um contraste venoso (gadolídeo), geralmenteinócuo.
    Quais são os inconvenientes da ressonância magnética?
    • Muitas pessoas não podem fazer esse exame, pois:
      • Têm em seu corpo algum metal que distorce as imagens;
      • Usam aparelhos que podem ter seu funcionamento alterado, como marca-passos, por exemplo;
      • São grandes demais para entrarem na máquina.
    • A claustrofobia de muitos pacientes torna o exame muito incômodo para eles.
    • O aparelho de ressonância magnética é relativamente barulhento.
    • Durante o exame de ressonância magnética o paciente deve ficar imóvel por longos períodos.
    • A ressonância magnética ainda é um procedimento custoso.
    ABC.MED.BR, 2012. Ressonância magnética: o que é? Como realizar o exame? Quais são os inconvenientes?. Disponível em: <http://www.abc.med.br/p/exames-e-procedimentos/327625/ressonancia-magnetica-o-que-e-como-realizar-o-exame-quais-sao-os-inconvenientes.htm>. Acesso em: 12 out. 2015.


Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)