MATEMATICA FINAMCEIRA

A matemática financeira utiliza uma série de conceitos matemáticos aplicados à análise de dados financeiros em geral.

Os problemas clássicos de matemática financeira são ligados a questão do valor do dinheiro no tempo (juro e inflação) e como isso é aplicado a empréstimos, investimentos e avaliação financeira de projetos. ^[1]

O tema também pode de ser aplicado a precificação de ações e de derivativos, mas esse tipo de aplicação não é tratada neste artigo.

Índice

  [esconder] 

• 1Conceitos
• 2Juros compostos
• 3Fórmulas e aplicações
  • 3.1Número fixo de pagamentos de mesmo valor
  • 3.2Número infinito de pagamentos de mesmo valor
  • 3.3Pagamentos não periódicos ou de valores diferentes
• 4Avaliação financeira de projetos
• 5Referências
• 6Ver também
• 7Ligações externas

Conceitos[editar | editar código-fonte]

• Principal, Capital ou Valor Presente: Valor que está sendo emprestado ou investido.
• Juro: Compensação paga pelo tomador do empréstimo (ou receptor do investimento) para ter o direito de usar o dinheiro até o dia do pagamento. Pode ser expresso em valor monetário ($) ou como uma taxa de juro (%).
• Saldo: É a soma do Principal com o Juro em um determinado momento.
• Parcela ou Pagamento: Valor pago pelo tomador do empréstimo (ou receptor do investimento).

Juros compostos[editar | editar código-fonte]

Ver artigo principal: Juro

Em geral, os problemas tratados pela matemática financeira consideram o regime de juros compostos ao invés de juros simples. Nesse regime, a fórmula usada é : ^[1]

${\displaystyle FV=PV(1+i)^{n},}$

ou, invertendo os termos,

${\displaystyle PV={\frac {FV}{(1+i)^{n}\,}},}$

onde

• ${\displaystyle FV:}$ Valor Futuro (do inglês Future Value)
• ${\displaystyle PV:}$ Valor Presente (do inglês Present Value)
• ${\displaystyle i:}$ Taxa de juros (do inglês Interest Rate)
• ${\displaystyle n:}$ Número de períodos

Fórmulas e aplicações[editar | editar código-fonte]

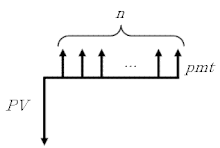
Número fixo de pagamentos de mesmo valor[editar | editar código-fonte]

Fluxo financeiro de um investimento (PV) com número fixo (n) de pagamentos de mesmo valor (pmt)

Esse pode ser o caso de financiamento de um bem de consumo, como o exemplo descrito na seção Exemplo de aplicação acima. ^[1]

O valor ${\displaystyle pmt}$ de cada parcela (ou pagamento periódico) pode ser considerado como o Valor Futuro (${\displaystyle FV}$) relativo a essa parcela. Portanto, a parcela do 3º mês, por exemplo, pode ser trazida a Valor Presente através da seguinte fórmula:

${\displaystyle PV_{3}={\frac {pmt}{(1+i)^{3}\,}}}$

Nesse caso, o Valor Presente (${\displaystyle PV}$) total é a soma dos "Valores Presentes" de todas as parcelas:

${\displaystyle PV=\sum _{k=1}^{n}{\frac {pmt}{(1+i)^{k}\,}}}$

Aplicando a fórmula da soma dos termos de uma progressão geométrica, chega-se a:

${\displaystyle PV={\frac {pmt}{i}}\left(1-{\frac {1}{(1+i)^{n}}}\right)}$

ou, invertendo os termos,

${\displaystyle pmt={\frac {PVi}{1-{\frac {1}{\left(1+i\right)^{n}}}}}}$

Esse exemplo considera que o primeiro pagamento ocorre 1 período depois do primeiro fluxo. Ou seja, entre ${\displaystyle PV}$ e ${\displaystyle pmt_{1}}$ existe um período. Caso o primeiro pagamento ocorra no período 0 (zero) ou depois de 1 período, a fórmula precisa ser adaptada.

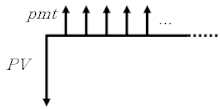
Número infinito de pagamentos de mesmo valor[editar | editar código-fonte]

Fluxo financeiro de um investimento (PV) com número infinito de pagamentos de mesmo valor (pmt)

Esse pode ser o caso de investimento que remunera um valor constante todo período, como, por exemplo, um título pré-fixado de dívida do governo. ^[2]

Da mesma forma como o exemplo anterior, o Valor Presente (${\displaystyle PV}$) total é a soma dos "Valores Presentes" de todas as parcelas, porém, considerando ${\displaystyle n=\infty .}$ Aplicando a fórmula da soma dos infinitos termos de uma progressão geométrica, chega-se a:

${\displaystyle PV={\frac {pmt}{i}}}$

Pagamentos não periódicos ou de valores diferentes[editar | editar código-fonte]

No caso de pagamentos diferentes em cada período, não é possível fazer essas simplificações. É necessário somar o Valor Presente de cada pagamento. ^[2]

Avaliação financeira de projetos[editar | editar código-fonte]

Projetos de investimento, como a abertura de uma loja, compra de uma máquina ou construção de uma estrada requerem um investimento financeiro inicial e é esperado que gerem resultado financeiro positivo ao longo do tempo. A matemática financeira ajuda a avaliar se o resultado esperado compensará o investimento inicial. ^[1]

Nesses casos, costuma-se usar uma notação um pouco diferente da que foi usada nesse artigo até aqui:

• ${\displaystyle CF}$ ou ${\displaystyle FC:}$ Fluxo de Caixa (Cash Flow em inglês). Valor monetário esperado em determinado período. Pode ser interpretado como o resultado financeiro (lucro) trazido pelo projeto em determinado mês ou ano.
• ${\displaystyle CF_{0}}$ ou ${\displaystyle FC_{0}:}$ Costuma ser usado para identificar o Investimento Inicial, que é feito no momento 0 (zero). Valor monetário a ser investido no projeto ao iniciá-lo. Normalmente é um valor negativo, caracterizando-o como uma despesa.
• ${\displaystyle NPV}$ ou ${\displaystyle VPL:}$ Valor Presente Líquido (Net Present Value em inglês). Soma do investimento inicial com os demais fluxos de caixa trazidos a valor presente.

${\displaystyle NPV=CF_{0}+{\frac {CF_{1}}{(1+i)}}+{\frac {CF_{2}}{(1+i)^{2}}}+{\frac {CF_{3}}{(1+i)^{3}}}+\cdots }$

A taxa de juros (${\displaystyle i}$) a ser usada no cálculo do valor presente líquido para avaliação de projetos é a taxa mínima de atratividade (TMA), que é a taxa de juros que representa o mínimo que o investidor se propõe a ganhar ao fazer o investimento.

Indicadores usados na avaliação financeira de projetos:

Payback: Tempo decorrido entre o investimento inicial e o momento no qual o lucro líquido acumulado se iguala ao valor desse investimento.

Taxa Interna de Retorno - TIR ou IRR (do inglês Internal Rate of Return): Valor da taxa de juro para que ${\displaystyle NPV}$ seja igual a 0 (zero).

Referências

1. ↑ ^{Ir para:a b c d} D.Sc. Marcus Vinicius Quintella Cury. «Matemática Financeira» (PDF). FGV. Consultado em 14 de setembro de 2016. Cópia arquivada (PDF) em 10 de dezembro de 2014
2. ↑ ^{Ir para:a b} Prof. Luiz Brandão (2006). «Matemática Financeira» (PDF). IAG / PUC-Rio. Consultado em 14 de setembro de 2016. Cópia arquivada (PDF) em 8 de agosto de 2014

Ver também[editar | editar código-fonte]

• Mercado de capitais
• Renda fixa

Ligações externas[editar | editar código-fonte]

O Wikilivros tem um livro chamado Matemática financeira

A Wikiversidade possui cursos relacionados a Matemática financeira

• Calculadora Financeira On-line- Versão on-line das principais fórmulas financeiras do Excel e OpenOffice Calc.
• Calculadora de Amortização- Calcula o pagamento dos juros e do principal bem como o acumulado dos juros e pagamentos.
• Calculadora HP-12C Virtual
• Matemática Financeira